Trying to shaking off the rust, I recently implemented a Mandelbrot plotter in Rust. I have to admin, despite being familiar with the pretty images, I never looked into the math behind it.

Mandelbrot Set

The Mandelbrot set is basically about convergence of a complex recursion. Assuming the series

$$ z_0(c) = 0 + 0i $$ $$ z_{n+1}(c) = z_n^2 + c $$

the Mandelbrot set is the set of numbers C, for which this series converges against a finite number for a sufficiently "high" number n (typically 100).

When plotting a Mandelbrot set, the pixel coordinate of the image is taken as complex input c. To determine if the series converges against a finite number, for each iteration it is checked if the norm of z is lower than an arbitrary number (e.g. 2), kind of a stability margin. If this is the case for all iterations until n, c is considered part of the Mandelbrot set (and is typically colored black).

Values of c, that lead to the iteration leaving the stability margin, are excluded from the Mandelbrot set. In plotting, usually a color map is applied that tells "how unstable" the series is, e.g. "how quickly" it diverges.

Rust Implementation

An iterative approach to calculating the iterations to instability for a given c and n = num_iterations can be found here:

type ComplexDouble = Complex<f64>;
fn mandelbrot(c: &ComplexDouble, num_iterations: u32) -> u32 {
    let mut diverge_count: u32 = 0;

    let mut z = ComplexDouble::new(0.0, 0.0);
    while diverge_count <= num_iterations {
        if z.norm() > 2.0 {
            return diverge_count;
        }

        z = z.powi(2) + c;
        diverge_count += 1;
    }
    num_iterations
}

To enable a nice color map, the function returns a u32 rather than a bool. If the returned value equals num_iterations, then c is part of the Mandelbrot set. If it is lower, it means it left the stability margin before calculating all iterations and therefore is unstable and not part of the Mandelbrot set.

I will leave out the details on how to plot the image, for the interested, the full code can be found on GitHub.

The final output looks like this: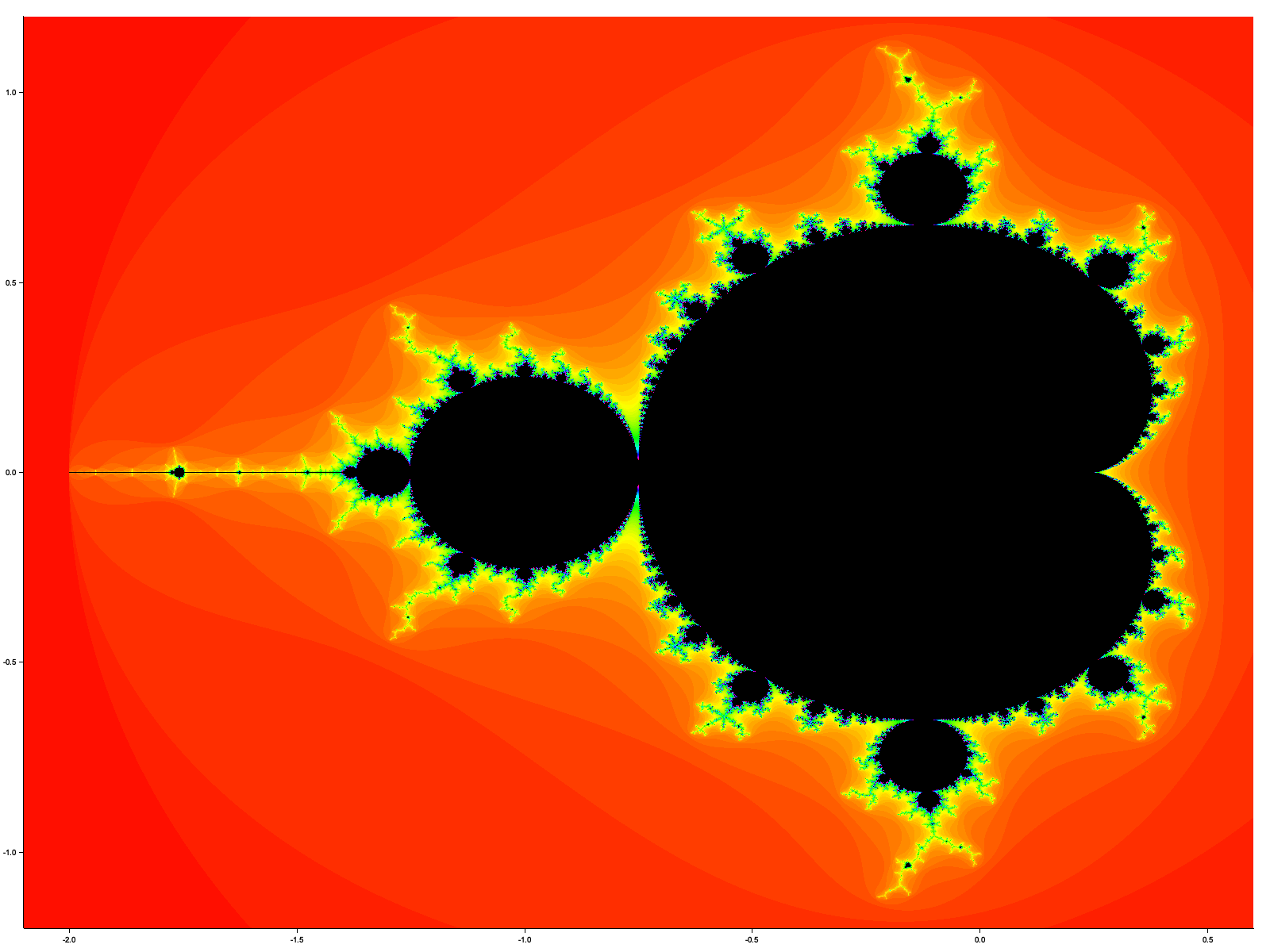

Different parts of the shape have been named and are worth to follow up outside this post. For me, it is astonishing that searching for stable values of c, there doesn't seem like a simple answer but a rather messy/chaotic structure, that can completely change for smallest variations of c. The Mandelbrot set is a fascinating mathematical phenomenon and there is much to explore further.